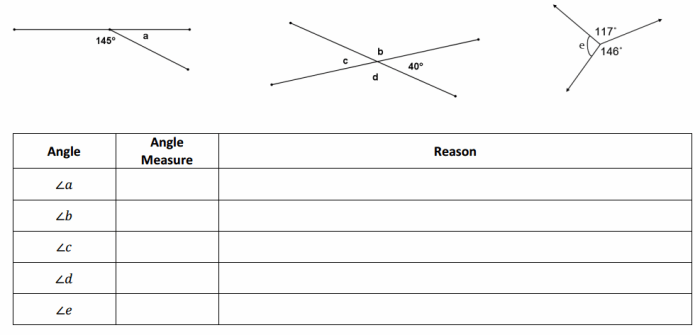
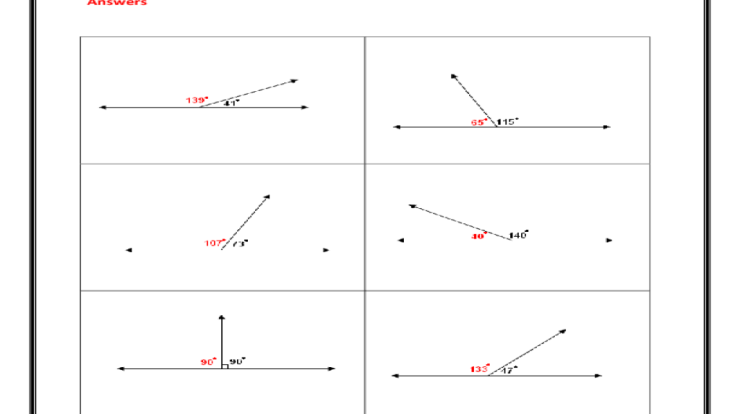
Axioms of equality common core geometry homework answers – Axioms of equality form the cornerstone of geometry, providing a set of fundamental principles that govern the relationships between geometric figures. These axioms play a crucial role in establishing the equality of geometric shapes, enabling mathematicians and engineers to construct precise and reliable geometric proofs.
In this comprehensive guide, we will explore the axioms of equality in the context of common core geometry, examining their significance, applications, and implications for geometric constructions. We will also delve into advanced concepts related to axioms of equality, highlighting their relevance to solving complex geometric problems and their practical applications in architecture, engineering, and design.
Introduction to Axioms of Equality
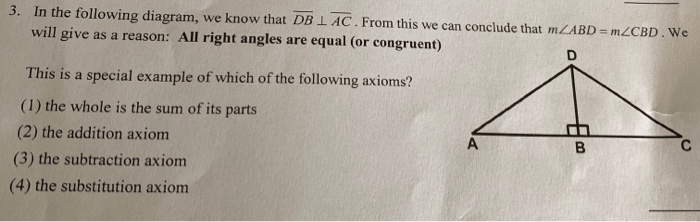
Axioms of equality are fundamental principles in geometry that establish the rules for determining whether two geometric figures are equal. They provide a foundation for geometric reasoning and ensure that geometric theorems and constructions are consistent and valid.
The axioms of equality play a crucial role in establishing the equality of geometric figures by providing a set of criteria that define when two figures are considered equal. These criteria include congruence, which involves the equality of shape and size, and similarity, which involves the equality of shape but not necessarily size.
Common Core Geometry Axioms of Equality, Axioms of equality common core geometry homework answers
- Reflexive Property:Every figure is equal to itself.
- Symmetric Property:If figure A is equal to figure B, then figure B is equal to figure A.
- Transitive Property:If figure A is equal to figure B and figure B is equal to figure C, then figure A is equal to figure C.
- Substitution Property:If figure A is equal to figure B, then figure A can be substituted for figure B in any geometric statement without changing the truth of the statement.
These axioms are used extensively in geometric proofs to establish the equality of figures. For example, the transitive property can be used to show that if triangle ABC is congruent to triangle DEF and triangle DEF is congruent to triangle GHI, then triangle ABC is congruent to triangle GHI.
Applications of Axioms of Equality
Axioms of equality have numerous applications in real-world scenarios, including:
- Architecture:Ensuring the symmetry and balance of buildings and structures.
- Engineering:Designing bridges, airplanes, and other structures that must meet specific geometric requirements.
- Design:Creating visually pleasing and functional objects that adhere to principles of equality and symmetry.
Frequently Asked Questions: Axioms Of Equality Common Core Geometry Homework Answers
What is the significance of axioms of equality in geometry?
Axioms of equality provide the foundation for establishing the relationships between geometric figures, enabling mathematicians and engineers to construct precise and reliable geometric proofs.
How are axioms of equality used in real-world applications?
Axioms of equality find practical applications in architecture, engineering, and design, where they are used to ensure the accuracy and precision of geometric constructions.
What are some advanced concepts related to axioms of equality?
Advanced concepts related to axioms of equality include the relationship between axioms of equality and other geometric concepts, such as congruence and similarity, as well as their use in solving complex geometric problems.